Computational Linear Algebra

Athul Sudheesh

1/1/22

Before we start…

Create dedicated project environments for different projects
Activate your project environment before you start working

using Pkg
Pkg.activate(".")

To add a package:

using Pkg
Pkg.add("PkgName")

Matrices are everywhere

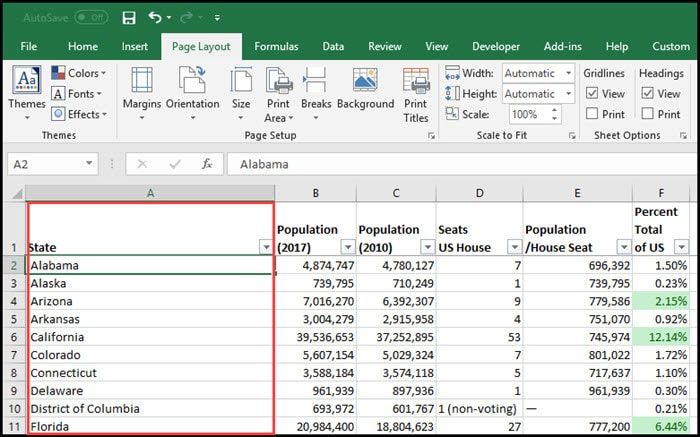
Excel

Tabular Data

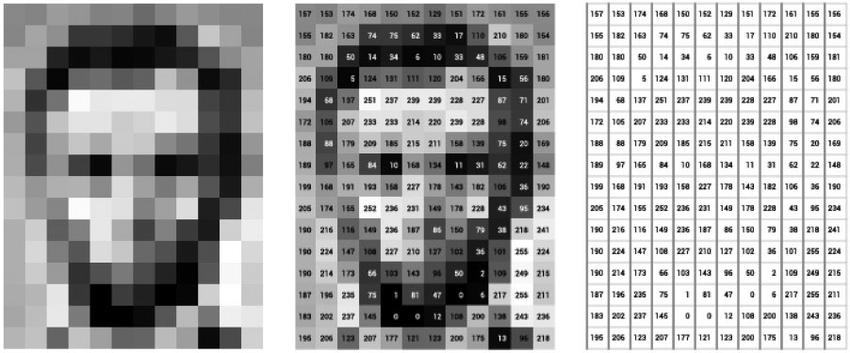
Images

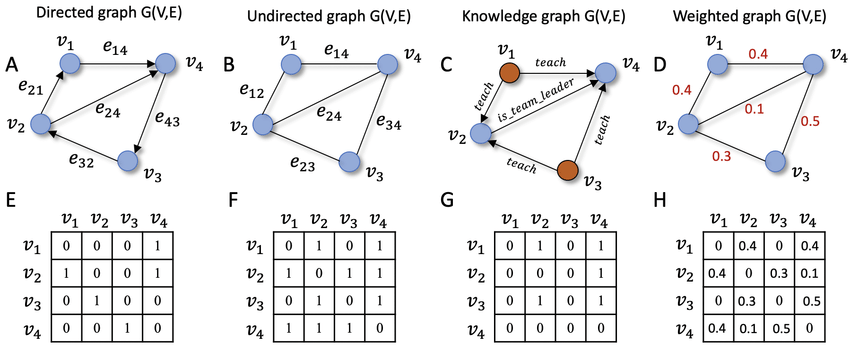
Graph Models

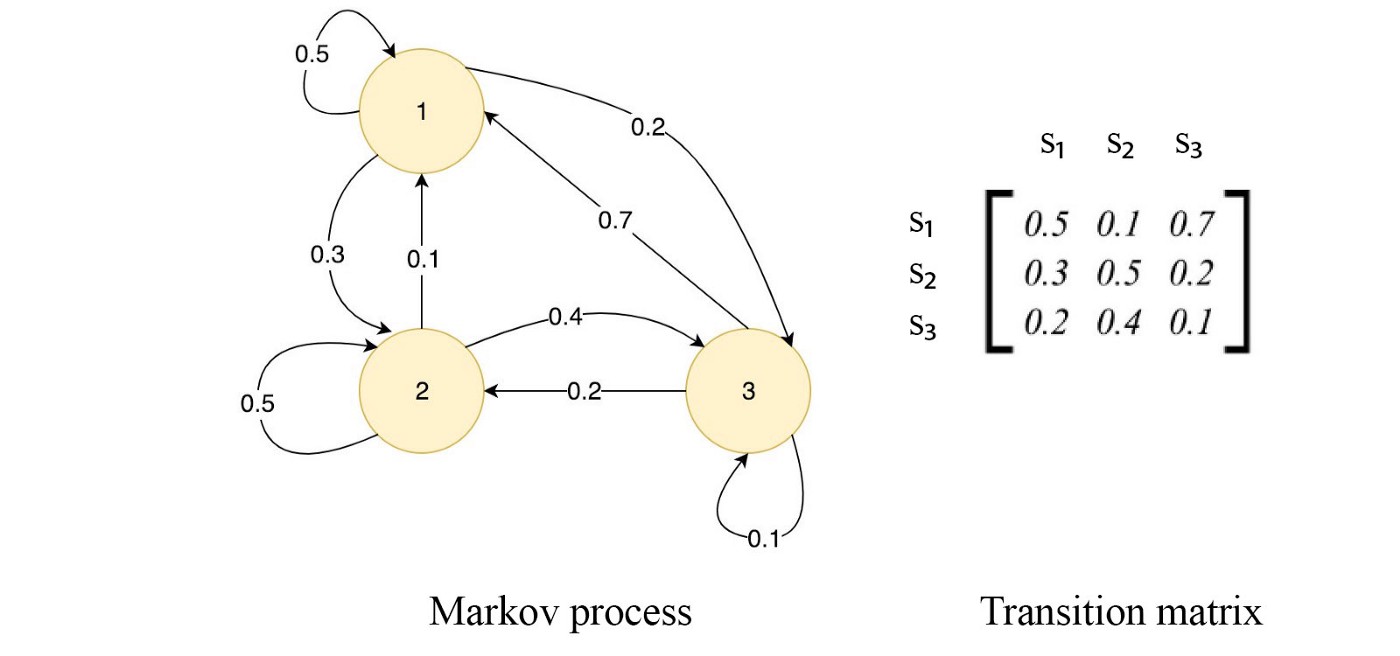
Markov Chains

Images as Matrices

Loading Images

# Packages for handling images 
using Images, ImageIO, ImageMagick 
# First time installation of Images package 
# could take couple of minutes.

Defining path to files

cat = joinpath(pwd(),"images", "cat.1.jpg")

Loading the image

catimg = load(cat)

Images as Matrices

Images are Multidimensional Matrices

[Height x Width] x Color

m,n = size(catimg)

(280, 300)

r = RGB.(red.(catimg), zeros(m,n), zeros(m,n))
g = RGB.(zeros(m,n), green.(catimg), zeros(m,n))
b = RGB.(zeros(m,n), zeros(m,n), blue.(catimg))

Images as Matrices

Images are Multidimensional Matrices

r .+ b .+ g

Many a times we do machine learning after turning images into GrayScale

Gray.(catimg)

Images as Matrices

Images are Multidimensional Matrices

Float64.(Gray.(catimg))

280×300 Matrix{Float64}:
 0.164706   0.164706   0.168627   0.172549   …  0.788235  0.768627  0.764706
 0.168627   0.168627   0.168627   0.172549      0.772549  0.756863  0.74902
 0.168627   0.168627   0.168627   0.168627      0.756863  0.752941  0.752941
 0.164706   0.160784   0.160784   0.156863      0.74902   0.760784  0.776471
 0.160784   0.156863   0.14902    0.145098      0.737255  0.760784  0.780392
 0.160784   0.156863   0.14902    0.141176   …  0.733333  0.752941  0.764706
 0.172549   0.164706   0.152941   0.145098      0.745098  0.756863  0.760784
 0.180392   0.172549   0.160784   0.14902       0.760784  0.772549  0.772549
 0.188235   0.176471   0.172549   0.172549      0.807843  0.803922  0.784314
 0.176471   0.168627   0.164706   0.168627      0.768627  0.756863  0.733333
 0.164706   0.156863   0.156863   0.164706   …  0.776471  0.756863  0.72549
 0.152941   0.145098   0.152941   0.160784      0.796078  0.776471  0.745098
 0.145098   0.141176   0.152941   0.164706      0.772549  0.760784  0.737255
 ⋮                                           ⋱                      
 0.105882   0.101961   0.0941176  0.0901961     0.188235  0.192157  0.207843
 0.0901961  0.0901961  0.0862745  0.0823529     0.203922  0.196078  0.192157
 0.0823529  0.0823529  0.0784314  0.0784314  …  0.282353  0.258824  0.247059
 0.0784314  0.0784314  0.0784314  0.0784314     0.360784  0.333333  0.317647
 0.0823529  0.0823529  0.0823529  0.0784314     0.243137  0.184314  0.211765
 0.0823529  0.0784314  0.0784314  0.0745098     0.215686  0.133333  0.137255
 0.0823529  0.0823529  0.0745098  0.0705882     0.188235  0.109804  0.109804
 0.0941176  0.0901961  0.0823529  0.0745098  …  0.160784  0.117647  0.137255
 0.109804   0.101961   0.0941176  0.0823529     0.121569  0.117647  0.160784
 0.121569   0.113725   0.0980392  0.0862745     0.101961  0.129412  0.192157
 0.121569   0.113725   0.0980392  0.0823529     0.12549   0.141176  0.184314
 0.121569   0.109804   0.0941176  0.0784314     0.160784  0.133333  0.12549

Image compression using SVD

using LinearAlgebra 
U,S,V = svd(Float64.(Gray.(catimg)));

Reconstructing the image using the singular values

RGB.(U*diagm(S)*V')

Image compression using SVD

function compressimg(n)
    RGB.(U[:,1:n]*diagm(S[1:n])*V[:,1:n]')
end

compressimg (generic function with 1 method)

compressimg(10)

Example 4.2.3 (page 110)

What’s the optimal number of features?

using GRUtils 
SNorm = S ./norm(S)
plot(1:length(S),SNorm, title="Scree Plot", 
        xlabel = "Singular Value IDs",
        ylabel = "Singular Values", grid=false)

SVD as recoding strategy (Image Example)

using Glob # For reading multiple files in a folder 
using Pipe: @pipe
function recodeimage(pathtoimage)
    # The following code block looks for .jpg/.JPG/.png/.PNG files and create a list of them 
    imagelist = glob("*.jpg", pathtoimage)  
    append!(imagelist,  glob("*.JPG", pathtoimage))
    append!(imagelist,  glob("*.png", pathtoimage)) 
    append!(imagelist,  glob("*.PNG", pathtoimage))


    # Algorithm for scree plot ===================================================================================
    # creating a temporary array of arrays to hold the numerical values of the grayscaled images 
    # temp[1] will have the grayscaled information of image 1, and so on...
    temp = Array{Array{Float64,2},1}(undef,length(imagelist))
    
    # @showprogress is a macro to print the progress of this loop when this function is run 
        for i in 1:length(imagelist)
        temp[i] = Float64.(Gray.(imresize(load(imagelist[i]),128,128))) 
        # @pipe is a macro for chaining multiple tasks
        # the next two blocks of code takes the image, converts it into grayscale and compute 
        # the singular values, then only the first n_singular values are stored in the recodedArray    
        #img_singluar = @pipe X |> Float64.(Gray.(_)) |> svdvals(_)[1:n_singularvlas]' 
        #recodedArray = vcat(recodedArray, img_singluar) 
    end
    
    # stacking individual images to create a giant image matrix 
    stackedX = vcat(temp...)
    println("Running Singular Value Decomposition...")
    U,S,V= svd(stackedX)
    S = S ./norm(S)
    screeplot(S)
    # ============================================================================================================
    
    # After examining the scree plot, the user decides the no. of singular values 
    n_singularvlas = input("No. of Features (due to bug in the code that reads user inputs, you might have to enter the no twice, if the program didn't run first time)")
    
    # Initializing an empty array to store the n_singular values of the images 
    recodedArray = Array{Float64}(undef, 0, n_singularvlas) 
    # computing singular values using only the first n_singulars 
    for imagearrays in temp
        img_singular = @pipe imagearrays |> svdvals(_)[1:n_singularvlas]'
        recodedArray = vcat(recodedArray, img_singular)
    end

    # Normalizing the singular values 
    recodedArray =  eachcol(recodedArray) ./ norm.(eachcol(recodedArray))
    # writing the array as a .csv file 
    filename = joinpath(pathtoimage, "image_recoded.csv")
    CSV.write(filename,  DataFrame(recodedArray, :auto), writeheader=true)
end

recodeimage (generic function with 1 method)