Linear Algebra

Part II: Representation and Applications

Representation: Images

Representation: Images

(334, 500)
utdimg[5,5]

utdimg[105,305]

utdimg[334,500]

Representation: Images

r = RGB.(red.(utdimg), zeros(m,n), zeros(m,n))
g = RGB.(zeros(m,n), green.(utdimg), zeros(m,n))
b = RGB.(zeros(m,n), zeros(m,n), blue.(utdimg))
r .+ b .+ g

Representation: Images

utdbnw = Gray.(utdimg)
(334, 500)
utdbnw[100:170, 260:490]
utdbnw[5,5]

utdbnw[105,305]

utdbnw[334,500]

Representation: Images

utdbnw = Gray.(utdimg)
(334, 500)
vec(Float64.(utdbnw))
167000-element Vector{Float64}:
 0.49019607843137253
 0.49019607843137253
 0.49411764705882355
 0.4980392156862745
 0.5019607843137255
 0.5058823529411764
 0.5098039215686274
 0.5098039215686274
 0.5137254901960784
 0.5176470588235295
 0.5215686274509804
 0.5254901960784314
 0.5294117647058824
 â‹®
 0.24313725490196078
 0.47843137254901963
 0.20392156862745098
 0.27450980392156865
 0.16470588235294117
 0.09411764705882353
 0.03529411764705882
 0.00392156862745098
 0.10588235294117647
 0.5411764705882353
 0.3215686274509804
 0.47058823529411764

Image Compression using SVD

using LinearAlgebra 
U,S,V = svd(Float64.(Gray.(utdbnw)))
RGB.(U*diagm(S)*V')

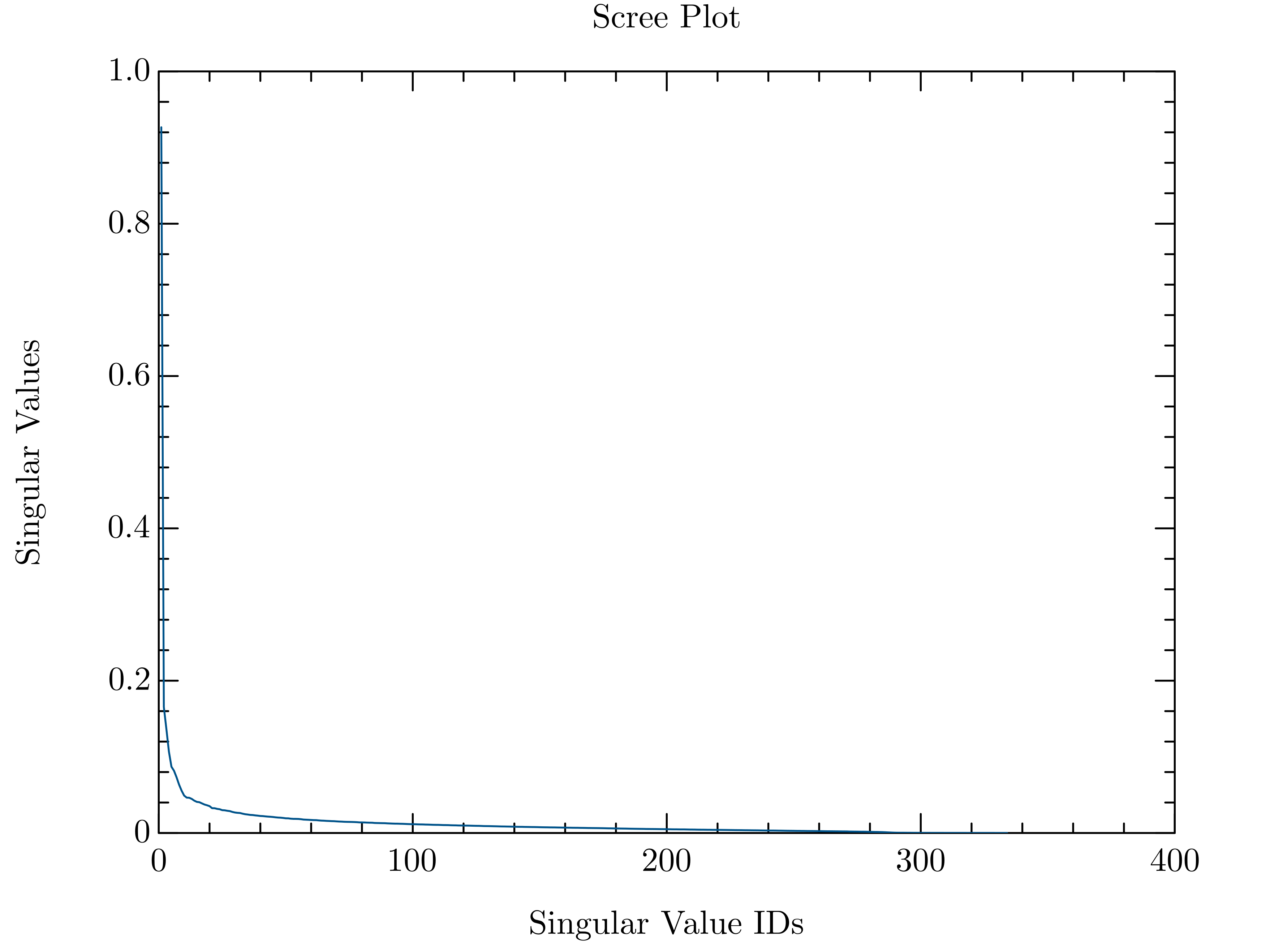
Image Compression using SVD

function compressimg(n)
    RGB.(U[:,1:n]*diagm(S[1:n])*V[:,1:n]')
end
compressimg (generic function with 1 method)
compressimg(20)

What’s the optimal number of features ?

What’s the optimal number of features ?

compressimg(10)
compressimg(20)
compressimg(30)