Linear Algebra

Part I: Vectors and Matrices

Why study Linear Algebra & Linear System?

It is the magic recipe behind everything computational
It is part of your everyday life!
- Search Algorithms
- Voice Assistants (Siri/Alexa)
- Image & Audio Editing Software
- ChatGPT & All other Deep Neural Networks

Image Editing using Linear Algebra

using Images, ImageIO, ImageMagick
utd = joinpath(pwd(),"utd.jpeg") 
utdimg = load(utd)
utdimg

Image Editing using Linear Algebra

Float64.(Gray.(utdimg))

334×500 Matrix{Float64}:
 0.490196   0.490196   0.490196   …  0.443137    0.443137   0.443137
 0.490196   0.490196   0.494118      0.447059    0.447059   0.447059
 0.494118   0.494118   0.494118      0.447059    0.447059   0.447059
 0.498039   0.498039   0.498039      0.45098     0.45098    0.45098
 0.501961   0.501961   0.501961      0.454902    0.454902   0.454902
 0.505882   0.505882   0.505882   …  0.458824    0.458824   0.458824
 0.509804   0.509804   0.509804      0.458824    0.458824   0.458824
 0.509804   0.509804   0.513725      0.462745    0.462745   0.462745
 0.513725   0.513725   0.513725      0.462745    0.462745   0.462745
 0.517647   0.517647   0.517647      0.462745    0.462745   0.462745
 0.521569   0.521569   0.517647   …  0.466667    0.466667   0.466667
 0.52549    0.52549    0.521569      0.466667    0.466667   0.466667
 0.529412   0.529412   0.52549       0.470588    0.470588   0.470588
 ⋮                                ⋱                         
 0.054902   0.0117647  0.0627451     0.423529    0.54902    0.243137
 0.152941   0.0666667  0.0705882     0.466667    0.52549    0.478431
 0.360784   0.196078   0.101961      0.141176    0.152941   0.203922
 0.341176   0.164706   0.0745098  …  0.0235294   0.152941   0.27451
 0.176471   0.0509804  0.027451      0.00392157  0.0745098  0.164706
 0.133333   0.0313725  0.0313725     0.0627451   0.0235294  0.0941176
 0.0588235  0.0862745  0.0156863     0.113725    0.0745098  0.0352941
 0.423529   0.388235   0.0627451     0.184314    0.105882   0.00392157
 0.333333   0.184314   0.0666667  …  0.243137    0.321569   0.105882
 0.298039   0.34902    0.235294      0.164706    0.423529   0.541176
 0.364706   0.235294   0.403922      0.180392    0.478431   0.321569
 0.196078   0.27451    0.258824      0.141176    0.521569   0.470588

Image Editing using Linear Algebra

Gray.(utdimg)

Gray.(utdimg) .+ 0.5

Image Editing using Linear Algebra

Gray.(utdimg)

Gray.(utdimg) .- 0.5

Image Editing using Linear Algebra

Gray.(utdimg)

Gray.(utdimg) .* 0.5

Image Editing using Linear Algebra

Gray.(utdimg)

Gray.(utdimg)[1:5:end,1:5:end]

Building Blocks of Linear Algebra

Scalars, c
- denoted by italics lowercase character
- 0D Array

c = 2

Vectors, \(\mathbf{x}= [ x_1, x_2, x_3]\)
- denoted by boldface lowercase character
  - elements of a vector are denoted by lower case characters with subscripts
  - subscripts denote the position of the elements in the vector
- 1D Array

# Column Vector 
x = [1,2,3]

3-element Vector{Int64}:
 1
 2
 3

# Row Vector 
x = [1 2 3]

1×3 Matrix{Int64}:
 1  2  3

Building Blocks of Linear Algebra

Matrices, \[\mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & c_{13} \\ a_{21} & a_{22} & a_{23}\\ \end{bmatrix}\]
- denoted by uppercase boldface character
  - elements of a matrix are denoted by lowercase character with subscripts
  - subscript denotes the row number and column number of the element
- 2D Array

A = [21 12 99;
    11 43 51]

2×3 Matrix{Int64}:
 21  12  99
 11  43  51

Tensors,
- N dimensional Array, where \(N > 2\)

Vectors

Vectors are points in space

Scalar Vector Multiplication

\(\mathbf{x} = [4,7]\)

\(\mathbf{x} \times 0.2 = [4*0.2, 7*0.2] = [0.8, 1.4]\)

Scalar Vector Multiplication

\(\mathbf{x} = [4,7]\)

\(\mathbf{x} \times -1 = [4* -1, 7* -1] = [-4, -7]\)

Vector Addition

\(\mathbf{x} = [1,2]\)

\(\mathbf{y} = [3,1]\)

Vector Addition

\(\mathbf{x} = [1,2]\)
\(\mathbf{y} = [3,1]\)

Vector Addition

\(\mathbf{x} = [1,2]\)
\(\mathbf{y} = [3,1]\)
\(\mathbf{x} + \mathbf{y} = \\ [1,2] + [3,1] = \\ [1+3, 2+1] = \\ [4,3]\)
In Julia:

x =[1,2]
y = [3,1]
x+y

2-element Vector{Int64}:
 4
 3

Vector Multiplication

There are several ways to multiply two vectors:

Dot Product (Inner Product), \(\qquad \mathbf{a} \cdot \mathbf{b}\)
Outer Product \(\qquad \qquad \quad \mathbf{a} \otimes \mathbf{b}\)
Cross Product \(\quad \quad \quad \qquad \mathbf{a} \times \mathbf{b}\)
Hadamard Product \(\quad \quad \quad \mathbf{a} \odot \mathbf{b}\)
Kronecker Product \(\quad \quad \quad \mathbf{a} \otimes \mathbf{b}\)

Note: These are not the same! Each method gives you a different output.

Vector Dot Product

\[ \mathbf{a} \cdot \mathbf{b} = \begin{bmatrix} a_{1} \\ \vdots \\ a_{n} \end{bmatrix} \boldsymbol{\bullet} \begin{bmatrix} b_{1} \\ \vdots \\ b_{n} \end{bmatrix} = \sum_{i=1}^{n} a_i b_i \]

Vector Dot Product

Consider two vectors, \(\mathbf{v} = \begin{bmatrix} 3 \\ -1 \\ 2 \end{bmatrix}\), \(\mathbf{w} = \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}\)

\[ \mathbf{v} \cdot \mathbf{w} = (3 \times 1) + (-1 \times 2) + (2 \times 1) \\ = 3 \]

using LinearAlgebra
v = [3 -1 2]
w = [1 2 1]
dot(v,w)

Alternatively,

v * w'

1×1 Matrix{Int64}:
 3

Vector Magnitude

Squareroot of the inner product of a vector with itself gives the magnitude of that vector

Distance between vectors

L1 Norm / Manhattan Distance

\(|\mathbf{u} -\mathbf{v}|_1 = \\ |3-1| + |1-2| = \\ |2| + |-1| \\ = 3\)

using LinearAlgebra
u = [1,2]
v = [3,1]
norm(u-v,1)

3.0

Distance between vectors

L2 Norm / Euclidean Distance

\(|\mathbf{u} -\mathbf{v}|_2 = \\ \sqrt{(3-1)^2 + (1-2)^2} = \\ \sqrt{(2)^2 + (-1)^2} =\\ \sqrt{4+1} = \sqrt{5} = 2.2361\)

using LinearAlgebra
u = [1,2]
v = [3,1]
norm(u-v,2)

2.23606797749979

Distance between vectors

Angular Separation

\[\cos \theta = \frac{\mathbf{u} \cdot \mathbf{v}}{||\mathbf{u}|| ||\mathbf{v}||} = \] \(\frac{(1 \times 3) + (2 \times 1)}{\sqrt{(1)^1+(2)^2} \times \sqrt{(3)^2+(1)^2}} = \frac{1}{\sqrt{2}}\)
\(\theta = \cos^{-1} (\frac{1}{\sqrt{2}}) = \\ 45^{\circ}\)

using LinearAlgebra
u = [1,2]
v = [3,1]
unorm = norm(u,2)
vnorm = norm(v,2)
acosd(dot(u,v) / (unorm*vnorm))

45.00000000000001

Distance between vectors

Angular Separation is a similarity measure

using LinearAlgebra
u = [1,2]
v = [1.5,3]
unorm = norm(u,2)
vnorm = norm(v,2)
acosd(dot(u,v) / (unorm*vnorm))

8.537736462515939e-7

Linear Neuron Model

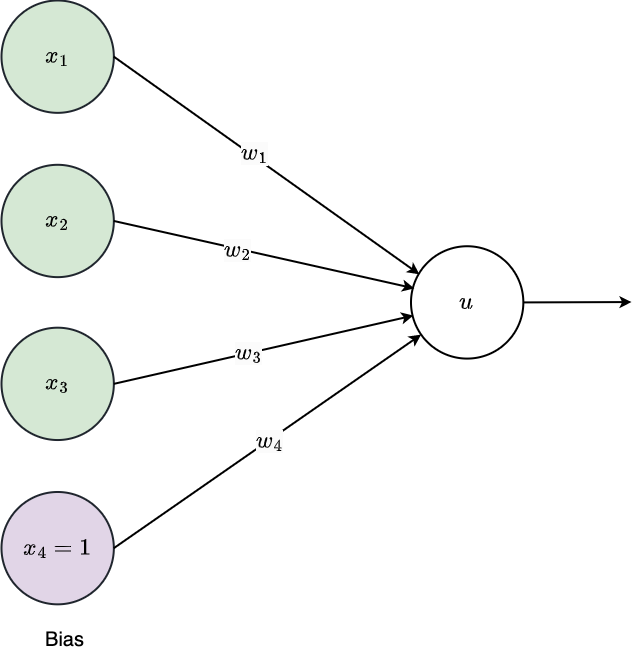
What is the output of this neuron model?

Matrices

Matrix Operations

Addition

M = [2 6;8 4]

2×2 Matrix{Int64}:
 2  6
 8  4

N = [1 0;-1 3]

2×2 Matrix{Int64}:
  1  0
 -1  3

M + N

2×2 Matrix{Int64}:
 3  6
 7  7

Multiplication by Scalar

3 * M

2×2 Matrix{Int64}:
  6  18
 24  12

Matrix Transpose

transpose(M)

2×2 transpose(::Matrix{Int64}) with eltype Int64:
 2  8
 6  4

Matrix-Vector Multiplication

As Linear Transformation

\(\mathbf{u} = \begin{bmatrix}4 \\1 \end{bmatrix}\)
Multiply \(\mathbf{u}\) by \(\mathbf{A} = \begin{bmatrix}1 & -3 \\1 & -1 \end{bmatrix}\)

Matrix-Vector Multiplication

As Linear Transformation

Matrix-Vector Multiplication

As Linear Transformation

\(\begin{bmatrix}1 & -3 \\1 & -1 \end{bmatrix} \begin{bmatrix} 4 \\ 1 \end{bmatrix} =\) \[ 4 \begin{bmatrix} 1 \\ 1 \end{bmatrix} + 1 \begin{bmatrix} -3 \\ - 1\end{bmatrix} =\]

\[\begin{bmatrix} 1 \\ 3 \end{bmatrix}\]

Matrix-Vector Multiplication

As Linear Transformation (Coordinate Transformation)

blue represents the transformed coordinates

Matrix-Vector Multiplication

What is the value of \(\mathbf{u}\)? \[\mathbf{u} = \begin{bmatrix} 3 & 4 & 5 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 2\end{bmatrix}\]

Matrix-Vector Multiplication

What is the value of \(\mathbf{u}\)? \[\mathbf{u} = \begin{bmatrix} 3 & 4 & 5 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 2\end{bmatrix}\]

\(= 1 \begin{bmatrix} 3 \\ 1 \end{bmatrix} + 0 \begin{bmatrix} 4 \\ 0 \end{bmatrix} + 2 \begin{bmatrix} 5 \\ 1 \end{bmatrix}\)

\(= \begin{bmatrix} 13 \\ 3 \end{bmatrix}\)

w = [3 4 5; 1 0 1]
v= [1,0,2]
w*v

2-element Vector{Int64}:
 13
  3

Connection Weight Matrix

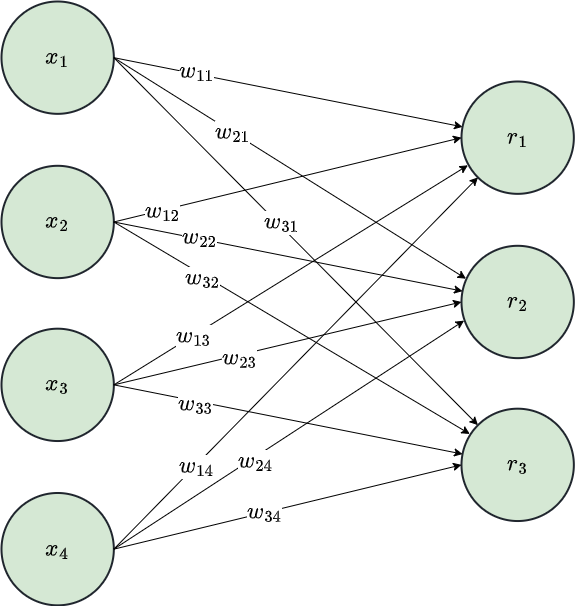
\[ \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24}\\ w_{31} & w_{32} & w_{33} & w_{34}\\ \end{bmatrix} \]

\[ \mathbf{r} = \mathbf{W} \mathbf{x} \]

Connection Weight Matrix

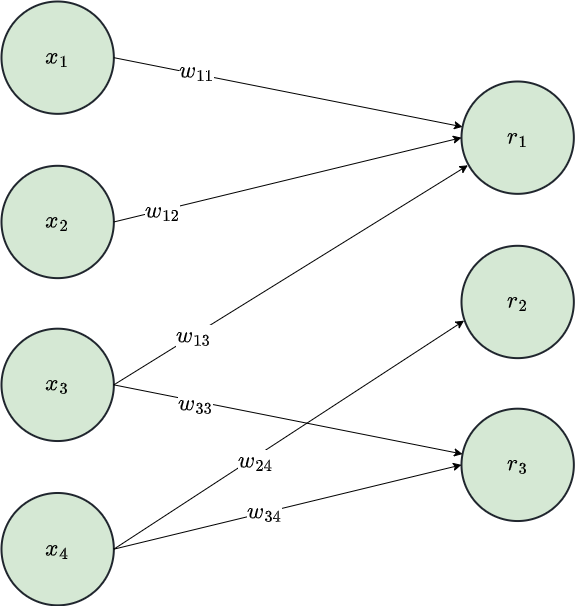
\[ \begin{bmatrix} w_{11} & w_{12} & w_{13} & 0 \\ 0 & 0 & 0 & w_{24}\\ 0 & 0 & w_{33} & w_{34}\\ \end{bmatrix} \]

\[ \mathbf{r} = \mathbf{W} \mathbf{x} \]

Connection Weight Matrix

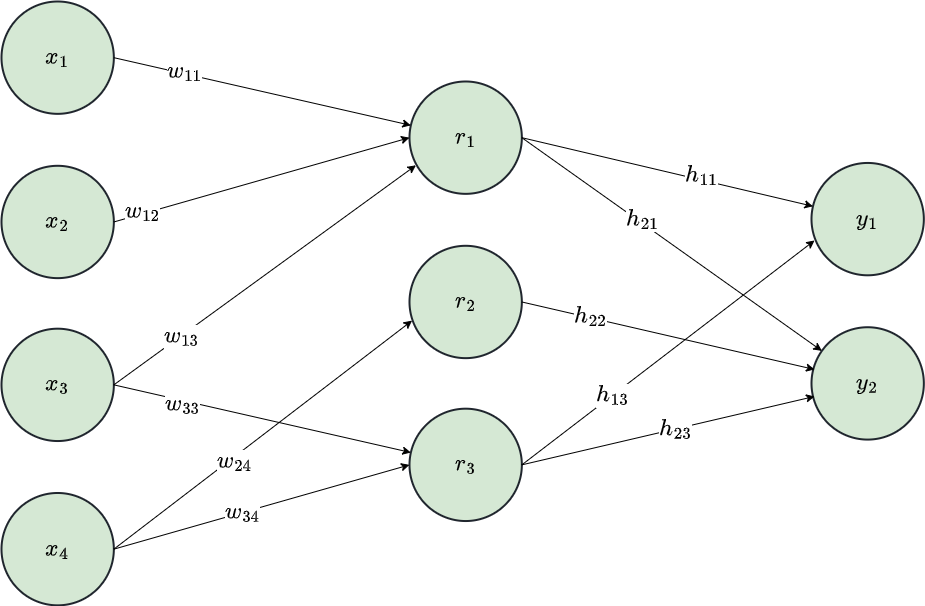
\[ \begin{bmatrix} w_{11} & w_{12} & w_{13} & 0 \\ 0 & 0 & 0 & w_{24}\\ 0 & 0 & w_{33} & w_{34}\\ \end{bmatrix} \]

\[ \mathbf{r} = \mathbf{W} \mathbf{x} \]

\[ \mathbf{y} = \mathbf{H} \mathbf{r} \]

Matrix-Matrix Multiplication

\(\begin{bmatrix} 1 & 2 \\ 3 & 1 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 1 & 2 \\ \end{bmatrix} =\)

\[\begin{bmatrix} \begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 3 \\ 1\end{bmatrix} & \begin{bmatrix} 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2\end{bmatrix} \\ \begin{bmatrix} 3 & 1 \end{bmatrix} \cdot \begin{bmatrix} 3 \\ 1\end{bmatrix} & \begin{bmatrix} 3 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2\end{bmatrix} \\ \begin{bmatrix} 1 & -1 \end{bmatrix} \cdot \begin{bmatrix} 3 \\ 1\end{bmatrix} & \begin{bmatrix} 1 & -1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2\end{bmatrix} \\ \end{bmatrix} = \]

\[\begin{bmatrix} 5 & 5 \\ 10 & 5 \\ 2 & - 1 \end{bmatrix}\]

A = [1 2; 3 1;1 -1]
B = [3 1; 1 2]
A * B

3×2 Matrix{Int64}:
  5   5
 10   5
  2  -1

Linear Algebra

Why study Linear Algebra & Linear System?

It is the magic recipe behind everything computational

Image Editing using Linear Algebra

Image Editing using Linear Algebra

Image Editing using Linear Algebra

Image Editing using Linear Algebra

Image Editing using Linear Algebra

Image Editing using Linear Algebra

Building Blocks of Linear Algebra

Building Blocks of Linear Algebra

Vectors

Vectors are points in space

Vectors are points in space

Scalar Vector Multiplication

Scalar Vector Multiplication

Vector Addition

Vector Addition

Vector Addition

Vector Multiplication

Vector Dot Product

Vector Dot Product

Vector Magnitude

Distance between vectors

L1 Norm / Manhattan Distance

Distance between vectors

L2 Norm / Euclidean Distance

Distance between vectors

Angular Separation

Distance between vectors

Angular Separation is a similarity measure

Linear Neuron Model

Matrices

Matrix Operations

Addition

Multiplication by Scalar

Matrix Transpose

Matrix-Vector Multiplication

As Linear Transformation

Matrix-Vector Multiplication

As Linear Transformation

Matrix-Vector Multiplication

As Linear Transformation

Matrix-Vector Multiplication

As Linear Transformation (Coordinate Transformation)

Matrix-Vector Multiplication

Matrix-Vector Multiplication

Connection Weight Matrix

Connection Weight Matrix

Connection Weight Matrix

Matrix-Matrix Multiplication